I have written several times over the years about the fascinating pattern known as Benford’s Law, which describes the weird pattern in the distribution of the first digit of numbers found in certain large datasets. It was famously noticed because the pages of books compiling tables of logarithms were more worn in the front, where logs started with 1 or 2, than in the back, where they started with 8 or 9.
If you want to learn more, the wikipedia article about Benford’s Law has a lot of detail – although, as if often the case with wikipedia articles about math topics, it’s more technical and dry than it should be for a general encyclopedia.
I bring this up because some people challenging the recent California gubernatorial recall election – some challenging the results before the election was held if you can believe it – were claiming that Benford’s Law shows that the result was rigged. Similar claims were flying after the 2020 presidential election when Trump and his supporters pretended he hadn’t lost, as I noted at the time.
One new wikipedia editor worried about misuse edited the wikipedia article right before the California vote to say: “It should be noted, however, that Benford’s Law cannot be used to critique a single data set (for example, if the results of a single opinion poll or election shows a larger difference, that in no way indicates a problem with that result).” But another editor removed it as being unsourced, which is a big black mark on wikipedia, so the article read as typical during the vote.
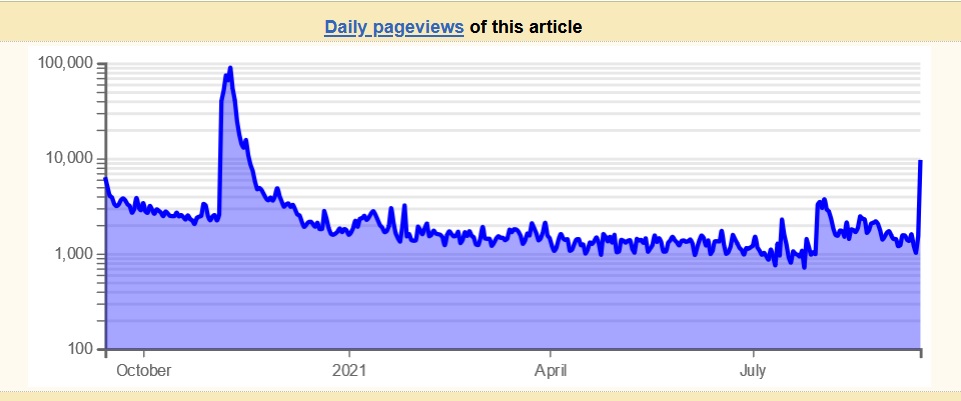
I was curious about how much attention the article got during the election. Fortunately wikipedia has a template to show page views over time. The chart above shows the views for the Benford’s Law article. You can see that viewing skyrocketed ten-fold during the California vote. You’ll also see, however, that it skyrocketed ten times as much during the last presidential vote.

 Return to the Concord Monitor
Return to the Concord Monitor
When I was in the Navy 50 years ago, I monitored Russian Navy communications. Ships would communicate with their base on a regular schedule. The problem was they could pop up on any frequency. I found that 40% if the time the first three digits of the frequency was a 1, 2, 3, or 4 and the last two or three digits were the favorite number of the guy setting up the scrambler. One ship I used to copy would always come up with low first numbers and one or two 7’s in the last numbers. I wonder whether this is an example of Benford’s law. It reminded me of the old law that if your last name began with a letter near the end of the alphabet you stood less of a chance of being called for jury duty. There was a simple explanation. The voter lists were kept in big data books and bindings. When you got halfway through the book it would flip over and close and you had to force the book open. Busy clerks didn’t have the time to mess with it so they would pick someone in the first half of the binder.